文章编号:10764时间:2024-09-29人气:
曲线拟合是 MATLAB 中一项强大的功能,它允许您通过一系列数据点拟合数学函数。这在数据分析、建模和预测中非常有用。
您需要准备要拟合的数据。确保数据已组织成矩阵,其中行代表数据点,列代表不同的变量。

下一步是选择要拟合数据的函数。MATLAB 提供了多种内置的拟合函数,包括线性、多项式、指数和正弦函数。选择最能代表您数据趋势的函数。
要拟合曲线,请使用以下语法:
fitobject = fit(x_data, y_data, fitType);
x_data
是自变量的数据。
y_data
是因变量的数据。
fittype
是您要使用的拟合函数类型。例如,要拟合线性函数,您可以使用以下代码:
fitobject = fit(x_data, y_data, 'poly1');曲线拟合完成后,您需要评估其准确性。MATLAB 提供了多种方法来评估拟合,包括:
可视化拟合曲线对于理解数据趋势和评估拟合准确性非常有用。要可视化拟合曲线,请使用以下语法:
plot(fitobject);让我们来看一个示例。假设我们有一个数据点集,如下所示:
x_data = [1, 2, 3, 4, 5];
y_data = [2, 4, 6, 8, 10];我们可以使用 MATLAB 拟合一条线性函数来这些数据点。以下是代码:
fitobject = fit(x_data, y_data, 'poly1');
拟合曲线如下所示:
R^2值为 0.99,表明拟合曲线与数据点拟合得很好。RMSE 值为 0.1,表明平均误差很小。
掌握 MATLAB 曲线拟合可以为您提供强大的数据分析工具。通过遵循这些简单的步骤,您可以轻松地拟合数据、评估拟合并可视化结果。
如果您有兴趣了解更多关于 MATLAB 曲线拟合的信息,请参考以下资源:
您好,这样的:一、 单一变量的曲线逼近Matlab有一个功能强大的曲线拟合工具箱 cftool ,使用方便,能实现多种类型的线性、非线性曲线拟合。 下面结合我使用的 Matlab R2007b 来简单介绍如何使用这个工具箱。 假设我们要拟合的函数形式是 y=A*x*x + B*x, 且A>0,B>0 。 1、在命令行输入数据:》x=[110.3323 148.7328 178.064 202. 224.7105 244.5711 262.908 280.0447 296.204 311.5475]》y=[5 10 15 20 25 30 35 40 45 50]2、启动曲线拟合工具箱》cftool3、进入曲线拟合工具箱界面“Curve Fitting tool”(1)点击“Data”按钮,弹出“Data”窗口;(2)利用X highlight=true>数据集名“Data set name”,然后点击“Create highlight=true>拟合曲线的类型,工具箱提供的拟合类型有:Custom Equations:用户自定义的函数类型 Exponential:指数逼近,有2种类型, a*exp(b*x) 、 a*exp(b*x) + c*exp(d*x) Fourier:傅立叶逼近,有7种类型,基础型是 a0 + a1*cos(x*w) + b1*sin(x*w) Gaussian:高斯逼近,有8种类型,基础型是 a1*exp(-((x-b1)/c1)^2) InterpolAnt:插值逼近,有4种类型,linear、nearest neighbor、cubic spline、shape-preserving Polynomial:多形式逼近,有9种类型,linear ~、quadratic ~、cubic ~、4-9th degree ~ Power:幂逼近,有2种类型,a*x^b 、a*x^b + c Rational:有理数逼近,分子、分母共有的类型是linear ~、quadratic ~、cubic ~、4-5th degree ~;此外,分子还包括constant型 Smoothing Spline:平滑逼近(翻译的不大恰当,不好意思) Sum of Sin Functions:正弦曲线逼近,有8种类型,基础型是 a1*sin(b1*x + c1) Weibull:只有一种,a*b*x^(b-1)*exp(-a*x^b) 选择好所需的拟合曲线类型及其子类型,并进行相关设置:——如果是非自定义的类型,根据实际需要点击“Fit options”按钮,设置拟合算法、修改待估计参数的上下限等参数;——如果选Custom Equations,点击“New”按钮,弹出自定义函数等式窗口,有“Linear Equations线性等式”和“General Equations构造等式”两种标签。 在本例中选Custom Equations,点击“New”按钮,选择“General Equations”标签,输入函数类型y=a*x*x + b*x,设置参数a、b的上下限,然后点击OK。
答案:
在MATLAB中进行曲线拟合,可以通过多种方法实现,其中常用的是使用MATLAB内置函数进行拟合。具体步骤如下:
1. 数据准备:首先,需要准备要进行拟合的数据,包括自变量和因变量。
2. 选择拟合函数:根据数据的特点和需要,选择合适的拟合函数,如多项式拟合、指数拟合、正弦拟合等。
3. 使用MATLAB内置函数进行拟合:MATLAB提供了许多内置函数,如`polyfit`、`fit`等,可以根据选择的拟合函数选择合适的函数进行拟合。
4. 绘制拟合曲线:使用MATLAB的绘图功能,将原始数据点和拟合曲线一起绘制出来,以观察拟合效果。
详细解释:
数据准备:
在进行曲线拟合之前,需要收集实验数据或者观测数据。 这些数据通常是成对出现的,包括自变量和因变量。 数据的准确性和可靠性对于拟合的结果至关重要。
选择拟合函数:
曲线拟合的目的是找到一个函数,这个函数能够最好地描述数据之间的关系。 根据数据的特性和问题需求,选择合适的函数形式。 例如,如果数据呈现出明显的指数增长趋势,那么指数函数可能是更好的选择;如果是周期性变化,则可以考虑正弦函数。
使用MATLAB内置函数进行拟合:
MATLAB提供了丰富的内置函数来进行曲线拟合。 例如,`polyfit`函数可以用于多项式拟合,`fit`函数可以用于更一般的函数形式拟合。 这些函数通常可以返回拟合参数的最佳估计值。
绘制拟合曲线:
为了直观地评估拟合效果,可以使用MATLAB的绘图功能将原始数据点和拟合曲线绘制在同一张图上。 通过对比,可以判断拟合曲线的质量是否满足要求。 同时,还可以计算拟合的残差、确定系数等指标来定量评估拟合效果。
以上即在MATLAB中进行曲线拟合的基本步骤和解释。
在MATLAB中,通过拟合工具cftool,我们可以方便地进行曲线拟合操作。以多项式拟合为例,所得的拟合函数为:
f(x) = p1*x^6 + p2*x^5 + p3*x^4 + p4*x^3 + p5*x^2 + p6*x + p7
其中,各参数的95%置信区间分别为:
拟合的优度指标显示,SSE(残差平方和)为8.865e-011,R-squared接近1,为0.9993,调整后的R-squared为0.999,RMSE(均方根误差)为2.219e-006,这表明拟合曲线对数据的描述非常精确。 通过这些参数和指标,我们可以对数据进行有效且精准的数学建模。
Matlab是一个很强大的数据处理软件,是人们进行数据分析的得力助手。 一般我们做社会调研或科学研究时,会得到很多实验数据。 当需要研究两个变量之间的关系时,经常要用到曲线拟合。 曲线拟合不仅能给出拟合后的关系式,还能用图形直观的展现出变量之间的关系。 其实用matlab做曲线拟合很便捷,下面将以两个变量(y=f(x))为例详细介绍:运行Matlab软件。 在工作空间中存入变量的实验数据。 具体如下:可以直接用矩阵来存放数据,直接在命令窗口输入x=[数据x1,数据x2,...,数据xn];y=[数据y1,数据y2,...,数据yn];当数据较多时,可以从excel,txt等文件中导入。 把数据存入工作空间后,在命令窗口中输入cftool,回车运行。 在这个拟合工具窗口的左边,选择变量,即分别选择x,y。 选择拟合的曲线类型,一般是线性拟合,高斯曲线,平滑曲线等,根据需要选择。 选择完后会自动完成拟合,并且给出拟合函数表达式。
拟合步骤:1、求(获)得一系列x,y对应值x=[...]y=[...]2、根据画出的曲线,,设定拟合函数fun=inline(a(1)+a(2)*exp(a(3)*x,a,x)3、初定x0的初值x0=[000]4、用拟合函数求出拟合系数a=lsqcurvefit(fun,x0,x,y)或a=nlinfit(x,y,fun,x0)用cftool的结果与实际是有较大的误差。 你不仿用二种获得的拟合函数,将已知值x代人,得到的yi,那个更接近已知值y。 一般用cftool工具箱,来判断拟合函数可能的形式。
内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/de5c0c914f713368dc8c.html,复制请保留版权链接!
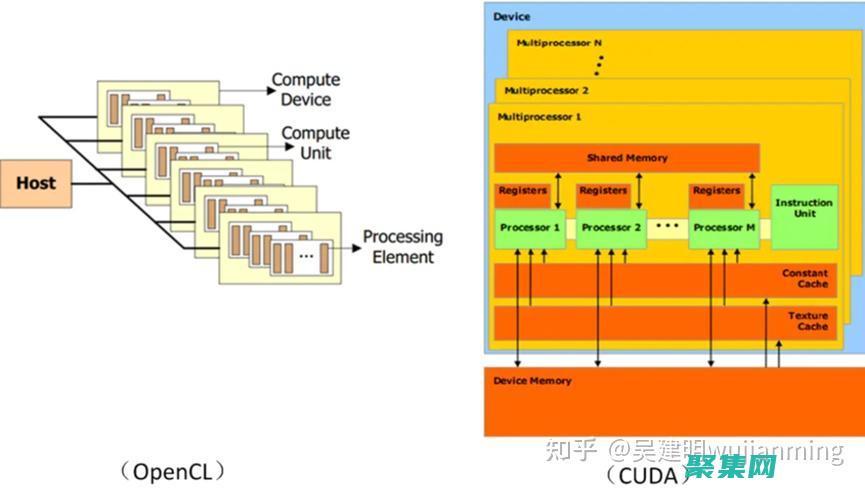
简介OpenCL,开放计算语言,是一种用于异构系统并行编程的开放标准,它允许开发人员利用CPU、GPU和其他加速器等异构计算资源来显著提高应用程序的性能,本文旨在将OpenCL与其他流行的并行编程语言进行对比,揭开它们的优势和局限性,比较标准我们将根据以下标准对OpenCL和其他并行编程语言进行对比,编程模型性能易用性支持平台编程模型...。
最新资讯 2024-09-28 16:28:44

前言嵌入式系统无处不在,从智能手机到汽车,再到医疗设备,随着物联网,IoT,的快速发展,对嵌入式系统工程师的需求正在不断增长,因此,掌握嵌入式系统设计至关重要,什么是嵌入式系统,嵌入式系统是一种专用于执行特定任务的计算机系统,它通常由一个微控制器或微处理器、存储器和输入,输出接口组成,嵌入式系统通常是实时操作的,这意味着它们必须能够快...。
最新资讯 2024-09-27 01:40:21

TaskParallelLibrary,taskpals,是一个用于.NET和.NETCore的高性能并行编程库,它提供了一组用于创建和管理并发任务的高级原语和数据结构,taskpals的优势高性能,taskpals旨在以最低的开销提供卓越的并发性能,易于使用,taskpals的API经过精心设计,易于使用和理解,即使对于并发编程新手...。
互联网资讯 2024-09-24 20:10:23
双精度定义在计算机科学中,双精度是一个数据类型,通常使用64位,8个字节,来存储浮点数,它能够表示比单精度浮点数更广泛的值范围和更高的精度,位布局一个64位双精度浮点数的典型位布局如下,符号位,1位,指数,11位,尾数,52位,尾数尾数是浮点数的实际数字部分,在双精度浮点数中,尾数使用二进制补码表示,并存储在52位中,它表示的值是...。
最新资讯 2024-09-23 02:03:31

简介SlideToggle是jQuery中一个强大的函数,它允许您以动画的方式显示或隐藏DOM元素,它可以通过单击按钮、悬停事件或任何其他事件触发,这是一种增强Web应用视觉吸引力和用户体验的有效方法,SlideToggle的语法SlideToggle函数的语法如下,$,selector,.slideToggle,[duration]...。
技术教程 2024-09-15 11:00:42

JavaScript的split,方法可根据指定的分隔符将字符串拆分为数组,语法str.split,separator,limit,其中,str是要拆分的字符串,separator是分隔符,可以是字符串或正则表达式,limit可选,指定要返回的子串数组的最大长度,不包括分隔符,示例,使用字符串分隔符拆分字符串conststr=H...。
互联网资讯 2024-09-14 22:09:25
HikariDataSourcedataSource=newHikariDataSource,dataSource.setJdbcUrl,jdbc,h2,mem,testdb,dataSource.setUsername,sa,dataSource.setPassword,returndataSource,注解扫描Spr...。
本站公告 2024-09-14 15:04:39
Scoping,变量的作用域规则,结论本教程为您提供了Perl编程的全面概述,通过练习和应用本教程中介绍的概念,您可以熟练掌握Perl,并创建强大的应用程序,记住,持续的练习和探索是精通编程的关键,...。
互联网资讯 2024-09-13 23:53:50
引言取整函数是一个重要的数学运算,它返回一个数的整数部分,舍弃小数部分,在数学和计算机科学中,它有着广泛的应用,从求解方程到处理数字数据,本文将深入探讨取整函数,详细说明其定义、性质和在各种领域中的应用,取整函数的定义取整函数,也称为floor函数或floor,x,,返回一个实数x的最大整数,它小于或等于x,数学表达为,floor,x...。
互联网资讯 2024-09-12 23:40:28
什么是VBA,VBA,VisualBasicforApplications,是微软开发的一种宏编程语言,可以嵌入到MicrosoftOffice应用程序,如Excel、Word、PowerPoint等,中,用于自动化任务、处理数据和创建自定义应用程序,VBA的优势易于学习,VBA语法简单,与VisualBasic类似,容易入门,强大的...。
最新资讯 2024-09-08 22:38:26

加油站是一个看似普通但实际上经常发生奇怪事件的地方,从夜晚闪烁的灯光到空荡荡的泵岛,这些地方往往笼罩着一层神秘的面纱,多年来,人们报告了无数与加油站有关的超自然遭遇,从鬼魂出现的幽灵般的目击事件,到令人不安的噪音和无法解释的故障,这些经历让无数人感到困惑和不安,汽油中的幽灵最著名的加油站幽灵之一被称为汽油中的幽灵,它是一个年轻妇女的幽...。
互联网资讯 2024-09-04 00:09:22
个人网站搭建,零成本与低成本的策略搭建个人网站的梦想,无需高额预算,这里为你揭示三种实用且简单的方法,首先,我们将探索完全免费的路径,然后转向那些在费用上可能有所妥协的选择,一、免费平台建站对于初级需求,你可以考虑利用第三方平台的个人空间功能,如WordPress的博客个人页面、知乎的个人主页或QQ的个人空间,这种方法无需专业知识,操...。
技术教程 2024-09-02 00:51:20