文章编号:10769时间:2024-09-29人气:
数据无处不在,它隐藏着宝贵的见解,可以帮助我们做出明智的决策。曲线拟合是揭示数据趋势的一种强大技术,它使我们能够用数学方程表示数据点之间的关系。
MATLAB 是一种用于技术计算和编程的强大工具。它提供了各种函数,可以很容易地进行曲线拟合,从探索和可视化数据到找到最佳拟合曲线并进行预测。
数据探索是曲线拟合过程的重要第一步。它使我们能够了解数据的性质,识别异常值并确定潜在的趋势。
MATLAB 提供了多种方法来可视化数据,包括:
plot
函数:绘制二维数据的折线图或散点图。
scatterplot
函数:创建散点图,其中每个点都用一个标记表示。
histogram
函数:显示数据的直方图,展示其分布。
一旦我们探索了数据,就可以开始选择合适的曲线拟合模型。MATLAB 提供了几种常见的模型,包括:
polyfit
函数
expfit
函数
logfit
函数
powerfit
函数
选择合适的模型需要考虑数据和拟合期望之间的平衡。我们可以在 MATLAB 中使用
fit
函数来拟合模型:
model = fit(xData, yData, 'poly1');
拟合模型后,我们需要评估其效果。MATLAB 提供了多种指标来评估拟合效果,包括:
我们可以在 MATLAB 中使用以下函数计算这些指标:
rSquared = model.Rsquared.ordinary;
rmse = sqrt(model.MSE);
maxRelativeError = max(abs(model.residuals)./abs(yData));
一旦我们评估了拟合模型,就可以使用它来进行预测。MATLAB 提供了多种用于预测新数据点的函数,包括:
predict
函数:使用拟合模型对新数据点进行预测。
plot
函数:绘制拟合曲线和预测值。
为了验证预测的准确性,我们可以在保留数据集上评估模型的性能。这有助于确保模型在新的、未见过的数据上的泛化能力。
除了曲线拟合,MATLAB 还可以轻松地求解线性方程组。这对于在各种应用中建模和分析系统非常有用,例如:
MATLAB 提供了多种方法来求解方程组,包括:
solve
函数:使用 LU 分解求解线性方程组。
linsolve
函数:使用 QR 分解求解线性方程组。
inv
函数:使用矩阵求逆求解线性方程组。
例如,我们可以使用
solve
函数求解以下方程组:
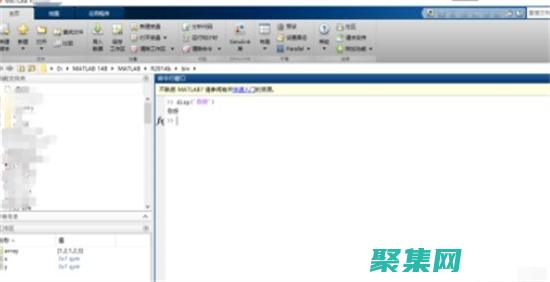
a = [1, 2, 3; 4, 5, 6; 7, 8, 9];
b = [10; 11; 12];
x = solve(a, b);
曲线拟合和方程求解是强大的技术,可以帮助我们从数据中提取有意义的信息。MATLAB 提供了各种函数和工具,使这些任务变得容易高效。通过探索、可视化、建模、评估、预测和验证,我们可以使用 MATLAB 揭示数据趋势,并做出数据驱动的决策。
1 多项式函数拟合:a=polyfit(xdata,ydata,n)其中n表示多项式的最高阶数,xdata,ydata为将要拟合的数据,它是用数组的方式输入.输出参数a为拟合多项式 的系数多项式在x处的值y可用下面程序计算.y=polyval(a,x)2 一般的曲线拟合:p=curvefit(‘Fun’,p0,xdata,ydata)其中Fun表示函数Fun(p,data)的M函数文件,p0表示函数的初值.curvefit()命令的求解问题形式是若要求解点x处的函数值可用程序f=Fun(p,x)计算.例如已知函数形式 ,并且已知数据点 要确定四个未知参数a,b,c,d.使用curvefit命令,数据输入 ;初值输 ;并且建立函数 的M文件(Fun.m).若定义 ,则输出又如引例的求解,MATLAB程序:t=[l:16]; %数据输人y=[ 4 6.4 8 8.4 9.28 9.5 9.7 9.86 10.2 10.32 10.42 10.5 10.55 10.58 10.6] ;plot(t,y,’o’) %画散点图p=polyfit(t,y,2) (二次多项式拟合)计算结果:p=-0.0445 1.0711 4.3252 %二次多项式的系数由此得到某化合物的浓度y与时间t的拟合函数。
m程序为:
g=[.37...9348];
h=[17.4 21.9826.0295 28..];
p=polyfit(g,h,3);
g2=5000:1000;
h2=polyval(p,g2);
plot(g,h,o,g2,h2);
xlabel(g);
title(H=a(0)+a(1)*G+a(2)*G^2+a(3)*G^3拟合曲线)
运行上面m文件得到结果如下:
0.0000 -0..0000 35.5845
也就是H=35.5845*G^3
在 MATLAB 中使用曲线拟合工具(Curve Fitting Tool)进行数据分析时,通常涉及两版工具的使用。 以下内容将详细介绍在 MATLAB 环境中,如何高效地应用曲线拟合工具进行数据拟合。
### 新版曲线拟合工具使用流程
新版曲线拟合工具提供了一种直观且易用的方法进行数据拟合,适用于单一曲线的拟合。
如果拟合曲线与数据点不符合预期,可以尝试调整曲线类型。
### 老版曲线拟合工具使用流程
对于希望在同一图表上展示多条曲线的用户,老版曲线拟合工具提供了方便的解决方案。
通过以上步骤,用户可以有效地使用 MATLAB 的曲线拟合工具进行数据分析,实现数据可视化和数学建模。 在拟合过程中,根据数据特点和需求,灵活选择合适的函数类型和调整参数,以获得准确的拟合结果。
x=[0.25:0.25:0.75,1:0.5:5,6:16]
y=[30,68,75,82,82,77,68,68,58,51,50,41,38,35,28,25,18,15,12,10,7,7,4];
plot(x,y,o)%做出数据的散点图。
然后调用基本拟合工具箱进行拟合,可以直观观察拟合效果,选择相对最好的拟合曲线。
拟合方程和图形如下:
Matlab是一个很强大的数据处理软件,是人们进行数据分析的得力助手。 一般我们做社会调研或科学研究时,会得到很多实验数据。 当需要研究两个变量之间的关系时,经常要用到曲线拟合。 曲线拟合不仅能给出拟合后的关系式,还能用图形直观的展现出变量之间的关系。 其实用matlab做曲线拟合很便捷,下面将以两个变量(y=f(x))为例详细介绍:运行Matlab软件。 在工作空间中存入变量的实验数据。 具体如下:可以直接用矩阵来存放数据,直接在命令窗口输入x=[数据x1,数据x2,...,数据xn];y=[数据y1,数据y2,...,数据yn];当数据较多时,可以从excel,txt等文件中导入。 把数据存入工作空间后,在命令窗口中输入cftool,回车运行。 在这个拟合工具窗口的左边,选择变量,即分别选择x,y。 选择拟合的曲线类型,一般是线性拟合,高斯曲线,平滑曲线等,根据需要选择。 选择完后会自动完成拟合,并且给出拟合函数表达式。
内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/832666cede5b943fad70.html,复制请保留版权链接!

LLVM,低级虚拟机,是一个开源编译器基础设施项目,它提供了一个与目标无关的优化和代码生成平台,它已经在各种编程语言、编译器和工具中得到广泛采用,并已成为编译器技术和优化领域的一个变革性工具,LLVM的核心组件LLVM由几个关键组件组成,中间表示,IR,LLVM使用一种称为中间表示,IR,的底层字节码格式来表示程序,IR与目标机器无...。
本站公告 2024-09-26 00:34:56
在当今快节奏的世界中,高效和简化任务至关重要,幸运的是,有许多在线工具可以帮助您提高工作效率,本文将为您提供一个全面的在线工具集,助您提升效率并简化日常任务,任务管理Asana,一款流行的任务管理工具,可供团队或个人使用,它允许您创建任务、设置截止日期、分配任务并跟踪进度,Trello,一款基于看板的任务管理工具,它使用拖放功能来组织...。
最新资讯 2024-09-25 22:00:56
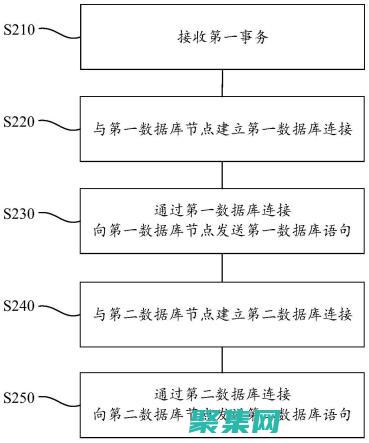
事务处理机制是数据库管理系统,DBMS,中的一项至关重要的功能,它确保数据库中的数据在应用程序执行的一系列操作过程中保持一致性和完整性,在事务处理机制中,BeginTransaction函数扮演着至关重要的角色,因为它标志着事务的开始,什么是事务处理机制,事务处理机制是一组规则和协议,用于管理数据库中的并发操作,确保数据的完整性和一致...。
最新资讯 2024-09-23 06:54:50
在软件开发中,测量字符串是开发人员面临的一项常见任务,但是,破解这些测量字符可能会带来挑战,特别是对于初学者,本指南将提供一个全面的步骤,指导您轻松破解测量字符串,步骤1,识别测量单位第一步是确定字符串中使用的测量单位,常见的单位包括,像素,px,百分比,%,emrem测量单位通常附加在字符的末尾,例如100px或50%,步骤2,将其...。
本站公告 2024-09-15 04:42:45

BSDC库MicrosoftVisualC,forLinuxEclipseCDTJetBrainsCLion使用C语言库和工具在C语言项目中使用库和工具时,请记住以下几点,选择满足您的项目需求的库和工具,按照库或工具的文档进行适当的安装和配置,使用库或工具时,遵守其许可条款,不断研究和了解C语言库和工具的最新发展,结论海量的C语言库...。
最新资讯 2024-09-13 11:22:08
前言电子商务已成为现代商业格局的关键组成部分,它为企业提供了向全球客户销售产品和服务的机会,同时为消费者提供了便利和广泛的选择,使用PHP开发电子商务网站是一种流行且有效的方法,因为PHP是一种健壮且广泛使用的脚本语言,本教程将指导您完成PHP电子商务开发的各个阶段,从基础到高级概念,您将学习如何使用PHP创建完整的电子商务网站,包括...。
本站公告 2024-09-11 19:32:26

小程序支付回调是微信小程序提供的一种功能,可以让开发者在用户完成支付后对支付结果进行处理,本文将介绍如何扩展小程序支付回调功能,自定义处理支付结果和业务场景,小程序支付回调在哪设置小程序支付回调地址需要在小程序管理后台设置,具体步骤如下,登录小程序管理后台,导航至,开发,>,接口设置,>,支付配置,在,支付回调,字段中输...。
互联网资讯 2024-09-11 01:40:03

简介γ分布,又称伽马分布,是一种连续概率分布,广泛应用于概率论和统计学中,其概率密度函数被定义为,f,x,=,x^α,1,e^,x,β,Γ,α,β^α,其中,α和β分别为形状参数和尺度参数,Γ,·,为伽马函数,函数图像γ分布密度的形状取決于其形状参数α,α<,1,曲线向右偏,具有右尾比左尾更长的分布,α=1,曲线呈指数分布,...。
互联网资讯 2024-09-09 08:31:37

Informix数据库管理系统提供了一系列强大的函数,用于处理字符串、数值和日期数据,这些函数使开发人员能够轻松地对数据进行各种操作,例如提取子字符串、格式化数字和转换日期,字符串函数SUBSTR,string,start,length,提取字符串的子字符串,从指定位置开始,指定长度,UPPER,string,将字符串转换为大写,...。
本站公告 2024-09-08 09:39:02

在竞争激烈的移动应用程序市场中,打造卓越的Android应用程序至关重要,从用户界面设计到后端实现,每个阶段都需要仔细考虑和熟练执行,本指南将引导您完成Android应用程序开发的整个过程,从构思到发布,1.设计阶段用户界面设计从用户调研开始,了解目标受众的需求和痛点,制定信息架构和线框图,以规划应用程序的布局和流程,使用现代设计原则...。
最新资讯 2024-09-07 20:50:42
前言PHP5.2.6是PHP5系列中发布的最后一个版本,由于其较旧且不再受支持,它不再适用于现代Web开发,但是,了解其优势和劣势对于理解PHP的演变以及它如何塑造了现代Web开发至关重要,优势稳定性,PHP5.2.6是一个经过时间考验且稳定的版本,在当时被广泛用于高流量网站,兼容性,它与许多旧版代码库兼容,使升级到较新版本的PHP变...。
互联网资讯 2024-09-07 14:37:06
引言在Linux环境中,Shell脚本是一种强大的工具,可以用来自动化任务,从而提升工作效率,通过编写和执行Shell脚本,用户可以将重复性或复杂的任务自动化,从而释放时间专注于更高价值的工作,本文旨在探讨LinuxShell自动化的优势和具体实现方法,Shell脚本的优势使用Shell脚本进行自动化具有以下优势,效率提升,自动化任务...。
互联网资讯 2024-09-07 12:26:53