文章编号:10765时间:2024-09-29人气:


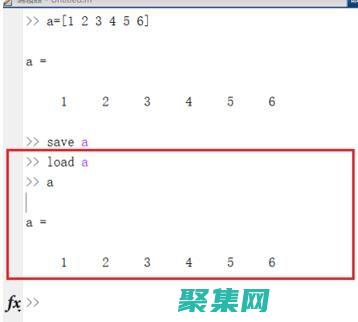
你的近似解析表达式为y=at+bt^2+ct^2是不是想写成为y=at+bt^2+ct^3但是实际拟合出来的表达式为y=a[3]+a[2]t+a[1]t^2+a[0]t^3会有个常数项的。
简单的讲,所谓拟合是指已知某函数的若干离散函数值,通过调整该函数中若干待定系数f(λ1, λ2,…,λ3), 使得该函数与已知点集的差别(最小二乘意义)最小。
如果待定函数是线性,就叫线性拟合或者线性回归(主要在统计中),否则叫作非线性拟合或者非线性回归。
表达式也可以是分段函数,这种情况下叫作样条拟合。
曲线拟合: #include
内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/08bcddad03a3ce5562de.html,复制请保留版权链接!
通过Xcode6探索Swift编程语言,为iOS开发注入速度和灵活性Swift概述Swift是一种由Apple开发的强大而现代化的编程语言,专为iOS、macOS、tvOS和watchOS等Apple平台设计,它是一种类型安全的编译语言,具有出色的性能和易用性,Swift于2014年推出,自那以来就因其易于学习、快速开发和强大的功能而...。
互联网资讯 2024-09-28 23:03:08
版本控制是管理软件项目代码更改的至关重要的工具,它使多个开发人员可以在同一个项目上协同工作,并跟踪代码库中随着时间推移所做的所有更改,Xcode中的版本控制Xcode6中内置了对版本控制的支持,这意味着您可以直接从Xcode管理您的代码版本库,而无需使用单独的版本控制工具,要开始使用Xcode中的版本控制,您需要创建一个Git存储库,...。
技术教程 2024-09-28 22:59:40
欢迎来到我们的网站,这里提供全面的网页设计资源,包括模板、图片、图标、字体、颜色方案等,我们致力于为设计师、开发人员和所有需要高质量设计素材的人提供一站式解决方案,description>,我们提供预先组装好的颜色方案,可以节省您的时间和精力,无论您是需要灵感还是完整的调色板,我们都可以满足您的需求,浏览颜色方案...。
最新资讯 2024-09-27 19:54:24

快速上手图像扩展和位块技术StretchBlt是一种位块传输技术,允许您在不同的内存位置之间高效地复制、拉伸和变形图像,它在图形编程和图像处理领域有着广泛的应用,在本文中,我们将带您快速浏览StretchBlt的基础知识,并展示如何使用它扩展和变形图像,StretchBlt原理StretchBlt基于以下原理,源和目标内存区域定义图像...。
互联网资讯 2024-09-27 13:17:08
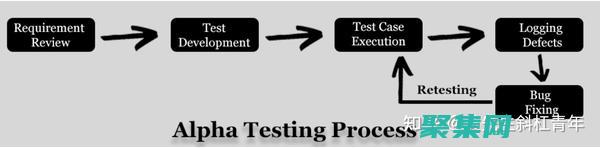
引言在软件开发生命周期中,Alpha测试和Beta测试是至关重要的阶段,有助于确保软件的质量和用户满意度,虽然这两个术语经常互换使用,但它们之间存在着关键差异,了解这些差异对于成功开展软件测试至关重要,Alpha测试定义Alpha测试是在软件开发的早期阶段进行的一种内部测试,通常由开发团队成员执行,该测试的目的是检查软件的基本功能和稳...。
技术教程 2024-09-25 03:03:13

基础滚动条的宽度和高度滚动条的宽度和高度可以通过`,webkit,scrollbar`伪元素来设置,默认情况下,滚动条的宽度为12px,高度为15px,可以通过设置其`width`和`height`属性来更改这些值,例如,要将滚动条的宽度设置为5px,高度设置为3px,可以使用以下代码,```css,webkit,scroll...。
本站公告 2024-09-15 09:06:09

因为这会导致脚本立即终止,可能导致丢失数据,错误注入,如果自定义错误处理程序没有正确编写,可能会导致错误注入,这使攻击者可以执行恶意代码,性能开销,使用自定义错误处理程序可能会增加性能开销,尤其是在处理大量触发错误的情况下,结论trigger,error函数是PHP中一个强大的工具,用于处理错误和警告,通过了解其运作方式和使用它的优势...。
互联网资讯 2024-09-13 22:28:05

示例代码以下示例代码演示了如何使用cURL函数从URL下载文件并将其保存到本地文件,结论cURL是一个强大的库,可用于执行各种URL请求,通过理解cURL函数的初始化过程,您可以轻松地下载文件、发送HTTP请求并处理响应,本指南提供了使用cURL函数和curl命令下载文件的全面概述,使您可以开始使用它来满足您的下载需求,...。
本站公告 2024-09-13 19:29:15
简介C语言是一种强大而通用的编程语言,广泛用于开发各种应用程序,本指南将介绍如何在PC或Mac上下载和安装C语言,步骤PC1.下载MinGW,MinGW,w64,MinGW是一个用于Windows平台的免费且开源的C编译器集合,访问MinGW网站,https,sourceforge.net,projects,mingw,w64,...。
互联网资讯 2024-09-12 08:03:38
支付回调是指当支付完成后,支付机构会向商家的服务器发起一个HTTP请求,告知商家支付结果,而支付回调地址是商家在支付时指定的,用于接收支付机构发起的HTTP请求的地址,支付回调字段支付回调请求中通常会包含以下字段,算法,具体验证方法请参考支付机构提供的文档,如何处理支付回调失败,支付回调失败时,商家系统可以重试接收回调请求,如果重试多...。
技术教程 2024-09-11 01:46:21

颜色在网页设计中扮演着至关重要的角色,它可以传达情绪、设置氛围并引导用户的行为,了解HTML颜色代码是任何Web开发人员必备的技能之一,HTML颜色代码格式HTML颜色代码使用十六进制表示法,由六个十六进制数字组成,前两个数字表示红色,中间两个数字表示绿色,后两个数字表示蓝色,例如,代码FF0000表示纯红色,而00FF00表示纯绿色...。
本站公告 2024-09-10 03:46:32
在编写代码时,效率和性能是需要考虑的重要因素,通过优化代码,可以显著提高应用程序的运行速度和响应能力,从而为用户提供更好的体验,本文将介绍多种编程调优技巧,帮助您提升代码效率和性能,这些技巧涵盖了从算法优化到数据结构选择等各个方面,算法优化算法是解决特定问题的步骤集合,选择合适的算法对于代码性能至关重要,以下是一些算法优化技巧,使用更...。
技术教程 2024-09-06 21:41:38