文章编号:10979时间:2024-09-29人气:

内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/deed6e2888a6928aebc2.html,复制请保留版权链接!

括号匹配概述括号是编程中用于将代码块分组的基本语法元素,正确匹配和使用括号对于编写可读、可维护的代码至关重要,括号成对出现,每种类型都有一个匹配的闭合括号,圆括号,`,`和`,`方括号,`[`和`]`花括号,`,`和`,`括号匹配的规则每个开括号都必须有一个匹配的闭合括号,闭合括号必须与它匹配的开括号出现在同一路径上,且次序正确,括号...。
技术教程 2024-09-27 08:31:31
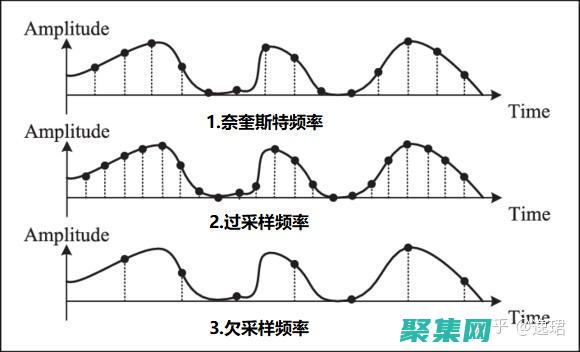
引言采样率是数字音频中最关键的参数之一,它决定了音频质量的清晰度和保真度,本文将探讨采样率的定义、单位和重要性,并说明如何选择合适的采样率,以满足不同的音频需求,采样率的定义采样率是指每秒采集的音频样本数量,以赫兹,Hz,为单位,它表示了模拟音频信号被数字化成离散数据点的速率,采样率越高,采样的数据点就越多,从而获得更详细的数字表示,...。
本站公告 2024-09-26 22:26:38

利用功能强大的个人网站设计模板,展示您的独特风格为什么使用个人网站设计模板,快速便捷,预制的模板可让您快速轻松地创建网站,无需从头开始,专业外观,模板是由专业设计师设计的,确保您的网站看起来既美观又专业,响应式设计,模板会自动调整为任何屏幕尺寸,确保您的网站在所有设备上都看起来很棒,可定制性,虽然模板提供了预构建的结构,但您仍然可以添...。
本站公告 2024-09-23 21:23:35
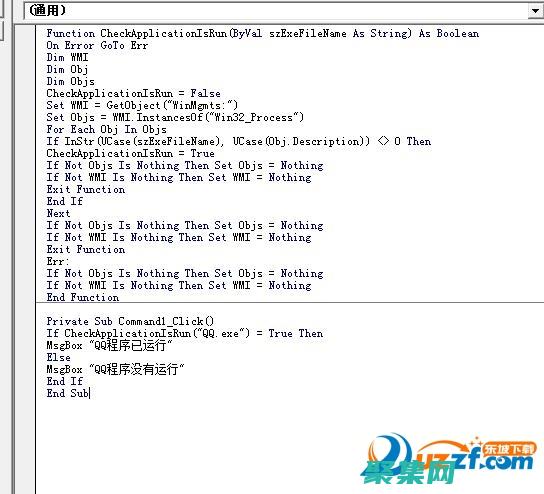
目录简介入门变量和数据类型运算符控制结构函数和过程模块和类错误处理高级主题资源简介VisualBasic,VB,是微软公司开发的一种流行的事件驱动编程语言,它以其易用性、直观性以及广泛的库而闻名,VB被广泛用于开发各种应用程序,包括桌面应用程序、网站和error,handling>,错误处理错误处理是识别和处理程序错误的机制,它有...。
本站公告 2024-09-12 12:04:16

引言Java是一种广泛使用的编程语言,拥有庞大的社区和生态系统,无论您是初学者还是有经验的开发者,在计算机上安装Java都至关重要,本教程将深入浅出地指导您完成Java安装过程,从下载JDK到设置环境变量,步骤1,下载Java开发工具包,JDK,前往Oracle官方网站下载Java开发工具包,JDK,选择与您的操作系统和体系结构匹配...。
技术教程 2024-09-10 04:42:21

中国的科技产业正在蓬勃发展,而编程是中国经济中一个日益重要的部分,编程中国是该国最大的编程社区之一,拥有超过1000万会员,在该平台的众多技术爱好者中,涌现了许多编程天才,他们正在用他们的技能塑造中国的未来,编程中国的杰出贡献者张雨锡,知名算法竞赛选手,在各大国际比赛中屡获殊荣,他也是一名出色的导师,帮助了许多学生提高编程水平,李锐,...。
最新资讯 2024-09-09 10:06:57

商业源码网,用商业级源码构建无缝应用程序引言在快速发展的数字世界中,企业需要高效、可靠且可扩展的应用程序来保持竞争力,商业源码网提供了商业级源码的解决方案,使企业能够快速、经济高效地构建无缝的应用程序,什么是商业源码,商业源码是预先构建、经过全面测试和可定制的软件组件,这些组件可用于开发各种应用程序,包括电子商务网站、内容管理系统、客...。
本站公告 2024-09-09 09:06:16

引言随机函数是编程中的一个重要工具,它允许您生成不可预测的值,这在许多应用程序中很有用,例如模拟、游戏和数据科学,生成随机数的机制生成随机数有两种主要机制,伪随机数生成器,PRNG,这些算法使用确定性的、可重复的过程来生成看似随机的数,虽然生成的数字技术上不是随机的,但它们通常足够随机以用于大多数目的,真正的随机数生成器,TRNG,...。
互联网资讯 2024-09-08 15:08:26

引言不完全Gamma函数是一个在概率和统计中具有广泛应用的特殊函数,它通过将Gamma函数与积分相结合来定义,提供了分析分布和概率的强大工具,不完全Gamma函数的定义不完全Gamma函数γ,s,x,定义为,γ,s,x,=∫0xts,1e,tdt其中s是一个复参数,x是一个实参数,不完全Gamma函数的性质不完全Gamma函数具有以下...。
技术教程 2024-09-07 13:38:45

灵应塔,又名北塔,位于四川省绵阳市绵山风景名胜区内,始建于明万历十一年,1583年,塔高58米,共12层,为八角形楼阁式砖塔,是绵山景区内标志性建筑之一,灵应塔的建造是为了纪念明朝抗倭名将戚继光,戚继光在任浙江巡抚期间,曾率军平定倭寇,保卫东南沿海,他去世后,人们为了纪念他的功绩,便在绵山之巅修建了这座宝塔,灵应塔的结构十分精巧,塔...。
互联网资讯 2024-09-05 03:08:10

前言红衣男,一个在网络上传播甚广的都市传说,它起源于网络论坛,讲述了一个身穿红衣的神秘男子,在深夜徘徊于城市街头,寻找猎物的恐怖故事,这个传说在互联网上流传多年,引发了无数人的恐惧和猜测,本文将深入探索红衣男都市传说的起源、传播和演变,揭开这个网络都市传说的神秘面纱,起源,网络论坛上的恐怖故事红衣男都市传说的起源可以追溯到2004年,...。
互联网资讯 2024-09-04 02:31:30

中国是一个拥有悠久历史和文化的国家,也流传着许多关于灵异事件的故事和传说,这些事件往往令人困惑和难以解释,引发了人们对超自然力量的猜测和争论,本文将深入调查中国发生的15起最令人困惑的灵异事件,揭示它们的背景、目击者的证词以及专家们的分析,这些事件将带我们进入一个神秘的世界,探索人性的黑暗面以及超自然力量的可能性,1.秦始皇陵之谜公元...。
互联网资讯 2024-09-04 01:34:11