文章编号:10663时间:2024-09-28人气:
在数学中,阶乘是一个基本概念,表示一个正整数乘以所有小于或等于它的正整数的乘积。它通常表示为 n!,其中 n 是正整数。
1000 的阶乘是一个巨大的数字,它的计算结果令人惊叹。1000 的阶乘表示为 1000!,其计算公式为:
1000! = 1 × 2 × 3 × ... × 1000
进行这个计算的结果是一个令人难以置信的庞大数字:
1000! = 40238726007709377354158490592
这个数字如此之大,以至于它无法用科学记数法表示,因为它的大约位数超过了 2565 位。
阶乘在数学和计算机科学中有着广泛的应用。以下是它的一些含义:
简单问题何必麻烦机哥哥哥给讲我1000面数数解要5偶数0.【5*2=10】1000/5=200.200呢答案否定呢些数解5.比2550...我知道5*5=25所25倍数贡献0.1000/25=40同道理贡献30谁呢125吧1000/125=8贡献405*5*5*5=面625倍数少呢仅已吧所终答案=249答案啦相信疑问贡献0甚麽200*140*28*31*4呢我告诉前面加比25倍数同5倍数125倍数同525倍数625倍数5、倍数故我没少算吧希望所帮助
在数学的瑰宝中,阶乘是一个简单而深邃的概念,它不仅与我们熟知的整数游戏相关,更延伸到了实数和复数的领域。 让我们一起走进伽马函数的定义,揭开阶乘插值问题的神秘面纱,以及欧拉天才般的解决之道。
1. 伽马函数的华丽登场伽马函数,就像一个数学界的魔术师,对实数域中的阶乘进行了优雅的扩展。 它不仅定义了非整数阶乘的值,还揭示了阶乘函数的连续性和延拓性。 对于实数x,gamma函数 (Γ(x)) 是这样一个神奇的函数,它在每个正实数上都与阶乘(n!)保持紧密联系。
2. 阶乘插值:欧拉的灵感火花想象一下,当我们在整数点(n)和(n+1)之间寻找阶乘的“中间步”,如((n+α)),欧拉的问题就显得尤为引人入胜。 他用复数的工具,比如欧拉公式,将阶乘这个看似简单的问题转化为了一种几何级数的计算。 他发现,((n+α)! = Γ(n+α+1)),这个公式就像一个桥梁,连接了整数阶乘和非整数阶乘的世界。
通过欧拉的巧妙计算,我们得知,((n+α)! = n! × Γ(α+1)),这个公式不仅解决了插值问题,还揭示了伽马函数在解决阶乘差值问题中的核心作用。
3. 伽马函数的历史长河哥德巴赫,那个曾经困扰于阶乘问题的伟大数学家,他的好奇心如同伽马函数的导火索,点燃了整个数学领域。 他提出的问题,如((1/2)!),挑战了我们对阶乘的传统理解。 然而,直到年轻的欧拉出现,用他的洞察力和创新思维,才真正解决了这个难题。
欧拉的解决之道,不仅解决了哥德巴赫的疑惑,也标志着伽马函数在数学史上的诞生,从此,阶乘的定义和计算范围得到了前所未有的拓宽。
4. 欧拉的智慧结晶:几何级数与伽马函数的交融欧拉通过几何级数的巧妙转换,将((n+1)! - n!)转化为一个积分,展示了(Γ(x+1) = x! = ∫ ^∞ e^(-t) t^x dt),这就是伽马函数的积分形式。这个公式揭示了阶乘与自然对数底数e的紧密联系,也使得我们能够以更广泛的角度理解阶乘的性质。
通过欧拉的计算,我们得以在实数领域无缝地定义阶乘,使得看似平凡的阶乘扩展到一个全新的数学世界。
比如5的位数是[log 5]=1,[]表示取整,10的位数是[log 10]+1=2,那么1000的阶乘的位数为[log 1000!]+1=[log 1+log 2+log 3+.......]+1,具体结果可以用程序算的
249个公式:当0 < n < 5时,f(n!) = 0; 当n >= 5时,f(n!) = k + f(k!), 其中 k = n / 5(取整)f(1000!) = 200 + f(200!) = 200 + 40 + f(40!) = 240 + 8 + f(8!) = 248 + 1 + f(1) =249 详细过程:问题描述给定参数n(n为正整数),请计算n的阶乘n!末尾所含有“0”的个数。 例如,5!=120,其末尾所含有的“0”的个数为1;10!= ,其末尾所含有的“0”的个数为2;20!= ,其末尾所含有的“0”的个数为4。 计算公式这里先给出其计算公式,后面给出推导过程。 令f(x)表示正整数x末尾所含有的“0”的个数,则有: 当0 < n < 5时,f(n!) = 0; 当n >= 5时,f(n!) = k + f(k!), 其中 k = n / 5(取整)。 问题分析显然,对于阶乘这个大数,我们不可能将其结果计算出来,再统计其末尾所含有的“0”的个数。 所以必须从其数字特征进行分析。 下面我们从因式分解的角度切入分析。 我们先考虑一般的情形。 对于任意一个正整数,若对其进行因式分解,那么其末尾的“0”必可以分解为2*5。 在这里,每一个“0”必然和一个因子“5”相对应。 但请注意,一个数的因式分解中因子“5”不一定对应着一个“0”,因为还需要一个因子“2”,才能实现其一一对应。 我们再回到原先的问题。 这里先给出一个结论: 结论1: 对于n的阶乘n!,其因式分解中,如果存在一个因子“5”,那么它必然对应着n!末尾的一个“0”。 下面对这个结论进行证明: (1)当n < 5时, 结论显然成立。 (2)当n >= 5时,令n!= [5k * 5(k-1) * ... * 10 * 5] * a,其中 n = 5k + r (0 <= r <= 4),a是一个不含因子“5”的整数。 对于序列5k, 5(k-1), ..., 10, 5中每一个数5i(1 <= i <= k),都含有因子“5”,并且在区间(5(i-1),5i)(1 <= i <= k)内存在偶数,也就是说,a中存在一个因子“2”与5i相对应。 即,这里的k个因子“5”与n!末尾的k个“0”一一对应。 我们进一步把n!表示为:n!= 5^k * k! * a(公式1),其中5^k表示5的k次方。 很容易利用(1)和迭代法,得出结论1。 上面证明了n的阶乘n!末尾的“0”与n!的因式分解中的因子“5”是一一对应的。 也就是说,计算n的阶乘n!末尾的“0”的个数,可以转换为计算其因式分解中“5”的个数。 令f(x)表示正整数x末尾所含有的“0”的个数, g(x)表示正整数x的因式分解中因子“5”的个数,则利用上面的的结论1和公式1有: f(n!) = g(n!) = g(5^k * k! * a) = k + g(k!) = k + f(k!) 所以,最终的计算公式为: 当0 < n < 5时,f(n!) = 0; 当n >= 5时,f(n!) = k + f(k!), 其中 k = n / 5(取整)。 计算举例 f(5!) = 1 + f(1!) = 1 f(10!) = 2 + f(2!) = 2 f(20!) = 4 + f(4!) = 4 f(100!) = 20 + f(20!) = 20 + 4 + f(4!) = 24 f(1000!) = 200 + f(200!) = 200 + 40 + f(40!) = 240 + 8 + f(8!) = 248 + 1 + f(1) =249
阶乘的计算方法
阶乘是一个数学概念,表示一个正整数与比它小的所有正整数的乘积。 具体来说,n的阶乘表示为n!。 例如,5! = 5 × 4 × 3 × 2 × 1 = 120。 计算阶乘的方法相对直接,遵循乘法原理。
详细解释:
1. 定义与基础理解:阶乘是一个数与比它小的所有正整数的乘积。 例如,3!是3与比它小的数的乘积,即3 × 2 × 1。
2. 计算步骤:

输入数字:首先确定需要计算阶乘的数字n。
乘法运算:从n乘以n-1开始,一直乘到1为止。 例如,计算5!时,从5开始乘以4,再乘以3,以此类推,直到乘以1。
得出结果:所有乘积的总和即为所求阶乘的结果。
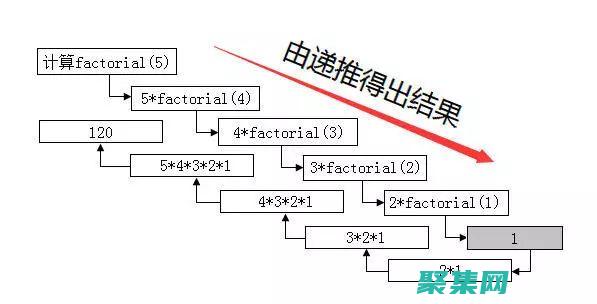
3. 注意事项:在计算阶乘时,数字的大小会直接影响结果的大小。 随着数字的增大,阶乘的结果会迅速增长,甚至可能超出常规计算工具的显示范围。 因此,在计算较大的阶乘时,需要特别小心。 此外,由于阶乘涉及大量的乘法运算,计算效率也是一个需要考虑的问题。
总的来说,计算阶乘是一个基础的数学运算,遵循乘法原理。 随着数字的增长,阶乘的计算会变得更为复杂和耗时。 在实际应用中,需要根据具体情况选择合适的计算方法。
内容声明:
1、本站收录的内容来源于大数据收集,版权归原网站所有!
2、本站收录的内容若侵害到您的利益,请联系我们进行删除处理!
3、本站不接受违法信息,如您发现违法内容,请联系我们进行举报处理!
4、本文地址:http://www.jujiwang.com/article/9c24bccdb0cb082469cf.html,复制请保留版权链接!

在竞争激烈的职场环境中,情绪智力,EI,已成为必不可少的软技能,对职业成功至关重要,EI指的是理解、管理和利用自己的情绪以及他人情绪的能力,它使个人能够在各种情况下驾驭人际关系,建立联系并取得积极成果,情绪智力的五个要素丹尼尔·戈尔曼博士,情绪智力之父,提出了情绪智力的五个核心要素,自知,识别和理解自己的情绪,并意识到情绪与思想和行为...。
技术教程 2024-09-27 07:53:53

简介音频录音机是一种用于捕获和记录声音的电子设备,它可以用于各种目的,包括音乐制作、播客录制、现场录音和语音备忘,如果您有兴趣录制音频,了解音频录音机的基础知识非常重要,本指南将带您从初学者到专家的五个阶段,帮助您选择和使用适合您需求的录音机,阶段1,选择录音机类型市场上有各种类型的录音机,每种类型都有其自身的优点和缺点,选择最适合您...。
本站公告 2024-09-26 02:20:41

简介PHP中的四舍五入函数是一个非常有用的工具,可以帮助我们对数字进行舍入操作,四舍五入的目的是将一个数字舍入到指定的小数位数,或者四舍五入到最接近的整数,函数语法PHP中的四舍五入函数有两种主要形式,`round,`函数,将数字舍入到指定的小数位数,`floor,`和`ceil,`函数,将数字分别向下或向上舍入到最接近的整数,...。
本站公告 2024-09-23 11:11:44

NaN,NotaNumber,是一个特殊值,表示一个无效的数字,当任何数字与NaN进行算术运算时,结果始终为NaN,NaN的定义NaN不是一个有效数字,因此不能参与普通的算术运算,它是一个特殊值,表示结果无效或未定义,NaN在算术运算中的表现当任何数字与NaN进行算术运算时,结果始终为NaN,这是因为NaN表示一个无效的数字,因此任何...。
技术教程 2024-09-23 02:31:35
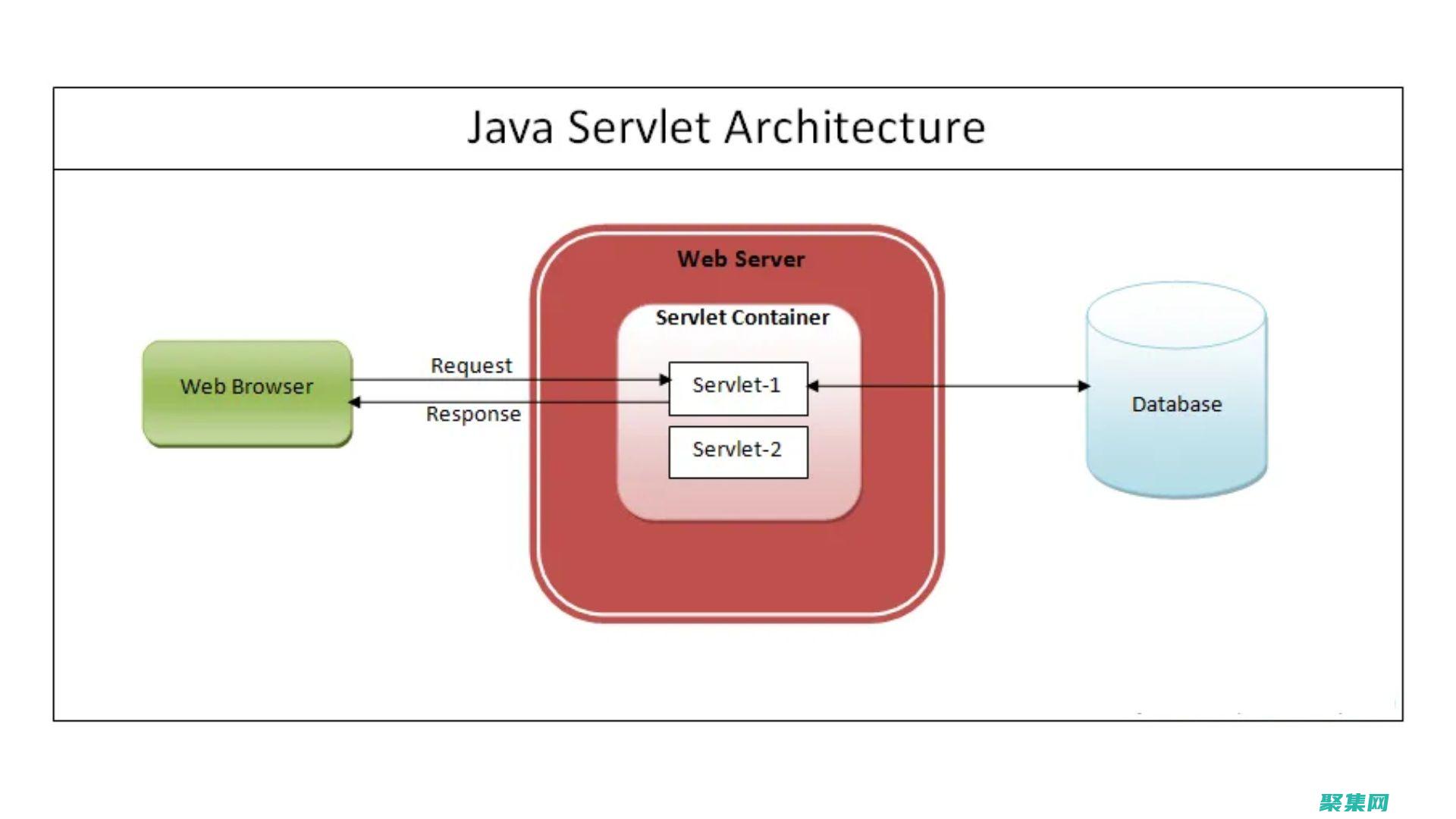
Servlet是一种Java编程模型,用于创建和管理动态web性和可维护性,使用依赖注入,使用依赖注入框架,例如Guice或Spring,注入组件依赖关系,提高代码的可测试性和松耦合性,单元测试Servlet,编写单元测试来验证Servlet的功能,确保其正确性和可维护性,使用日志记录框架,使用日志记录框架,例如Log4j或Logba...。
本站公告 2024-09-16 23:31:05

body,font,family,Arial,Helvetica,sans,serif,font,size,16px,h1,font,size,24px,margin,bottom,20px,h2,font,size,18px,margin,bottom,15px,ul,list,style,type,none,padding,...。
互联网资讯 2024-09-15 13:31:17

>,includeintmain,intn,scanf,%d,&,n,for,inti=1,i<,=n,i,=2,printf,%d,i,printf,\n,return0,4.2给定一个整数数组,编写一个C程序求数组中元素的最大值,includeintmain,intarr[]=,1,3,5,7,9...。
互联网资讯 2024-09-13 14:59:05

引言在当今竞争激烈的数字环境中,网站性能已成为确保业务成功的关键因素,一个速度缓慢、响应迟钝的网站可能会导致访问者流失、转化率低和收入损失,为了帮助您解决这些挑战,我们很高兴为您提供经过优化的ASP源代码,旨在显著提升您的网站性能,ASP源代码的优势ASP,活动服务器页面,是一种强大的服务器端技术,可用于创建动态Web应用程序,我们的...。
技术教程 2024-09-06 17:26:49

简介GCC,GNUCompilerCollection,是一个强大的开源编译器集合,用于编译各种编程语言,包括C、C,、Fortran和Ada,GCC编译器源码是一个庞大且复杂的代码库,理解它的内部原理对于深入理解编译器的运作方式以及优化代码性能至关重要,GCC编译原理编译规则GCC编译原理被组织成一系列清晰定义的阶段,每个阶段负责...。
本站公告 2024-09-05 18:47:34
所有模板均采用响应式设计,可在任何设备上无缝工作,这意味着无论您使用的是台式机、笔记本电脑、平板电脑还是智能手机,该网站都将自动调整大小以适合您的屏幕,这确保了用户无论使用什么设备都能获得最佳体验,响应式设计有许多优点,包括,它消除了为不同设备创建单独网站的需要,从而节省了时间和金钱,它提供了无缝的用户体验,无论用户使用什么设备,它有...。
技术教程 2024-09-05 10:32:49

汶川大地震是一场毁灭性的自然灾害,夺去了近7万人,其中包括许多儿童,地震后的废墟中,幸存者们不仅要承受巨大的身体和心理创伤,还要面对失去亲人的悲痛,在灾后的岁月里,许多幸存者报告说,他们与逝去的亲人进行了超自然联系,这些联系形式多样,包括梦境、幻觉、直觉,甚至肉眼可见的灵体出现,对于这些经历,专家们给出了不同的解释,一些人认为,它们是...。
互联网资讯 2024-09-04 02:05:42

前言双鱼玉佩,一块神秘的古代文物,传说中拥有强大的超自然力量,其起源不明,但关于它的故事和传说却流传已久,据传,双鱼玉佩可以带来好运和财富,但同时也可以招致邪恶和厄运,图片记录最近发现的一组图片记录揭示了双鱼玉佩背后的黑暗秘密,这些图片展示了一个由邪恶力量控制的人的生活,该人获得了双鱼玉佩并遭受了可怕的后果,邪恶寓言图片中记录的寓言讲...。
互联网资讯 2024-09-03 00:55:10