阐述千位阶乘：从基本概念到惊人结果 (1000的阶乘多少位)

什么是阶乘？

阶乘是一种数学运算，通常由感叹号 (!) 表示。对于一个正整数 n，n 的阶乘表示所有从 1 到n 的正整数的乘积。例如：

3! = 3 x 2 x 1 = 6
5! = 5 x 4 x 3 x 2 x 1 = 120

千位阶乘

千位阶乘指的是 1000 的阶乘，用 1000! 表示。计算 1000! 的值是一个巨大的挑战，但它可以表示为一个非常大的数：

1000! =40238726007709377354158490592...

惊人的结果

千位阶乘具有令人难以置信的大小和一些惊人的结果：

• 位数：1000! 的位数约为 2568 位，远高于任何标准计算器所能显示的范围。
• 末尾的零：1000! 中末尾的零有 249 位，这是因为阶乘运算中包含了大量的 10。
• 原子：假设一个原子的大小约为 10 ^-10 米，那么用 1000! 写下的数字将延伸到大约 10 ²⁴⁶⁵ 光年的距离，这比已知宇宙的直径要大得多。
• сравнение：1000! 远比已知宇宙中所有原子的总数还要大，后者估计约为 10 ⁸⁰ 。

计算 1000!

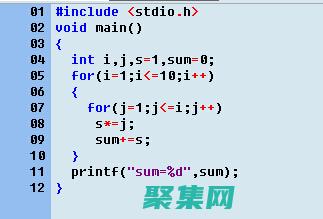
计算 1000! 的确切值是一个相当复杂的任务。可以使用以下步骤执行近似计算：

1. 计算 1000! 的对数（底数为 10）。
2. 使用对数函数的反函数找到 1000! 的近似值。

使用这种方法，我们可以获得 1000! 的近似值为 4.02 x 10 ²⁵⁶⁷ 。

应用

千位阶乘在数学和科学中没有实际应用。它作为一个展示指数增长的惊人例子，以及人类试图理解和量化难以想象的大数字的能力。

结论

千位阶乘是一个巨大的数字，超越了我们日常经验的范围。它的计算揭示了数学和数字世界中存在的令人难以置信的广度和深度。

---

1000!是什么意思啊，！作用是什么

阶乘吗？还是非的意思？“1000！”后面没有任何运算符，或是字符？ 如果只是1000！就是1000阶乘，这个数字的结果是很大的，1一直乘到1000如果有后续运算符或是字符意思就是非的意思，例如1000！=3,含义是1000不等于3

思想之翼:一千的阶乘"1000!"算出来有多少个零?

249个公式：当0 < n < 5时，f(n!) = 0; 当n >= 5时，f(n!) = k + f(k!), 其中 k = n / 5（取整）f(1000!) = 200 + f(200!) = 200 + 40 + f(40!) = 240 + 8 + f(8!) = 248 + 1 + f(1) =249 详细过程：问题描述给定参数n（n为正整数），请计算n的阶乘n！末尾所含有“0”的个数。 例如，5！=120，其末尾所含有的“0”的个数为1；10！= ，其末尾所含有的“0”的个数为2；20！= ，其末尾所含有的“0”的个数为4。 计算公式这里先给出其计算公式，后面给出推导过程。 令f(x)表示正整数x末尾所含有的“0”的个数，则有： 当0 < n < 5时，f(n!) = 0; 当n >= 5时，f(n!) = k + f(k!), 其中 k = n / 5（取整）。 问题分析显然，对于阶乘这个大数，我们不可能将其结果计算出来，再统计其末尾所含有的“0”的个数。 所以必须从其数字特征进行分析。 下面我们从因式分解的角度切入分析。 我们先考虑一般的情形。 对于任意一个正整数，若对其进行因式分解，那么其末尾的“0”必可以分解为2*5。 在这里，每一个“0”必然和一个因子“5”相对应。 但请注意，一个数的因式分解中因子“5”不一定对应着一个“0”，因为还需要一个因子“2”，才能实现其一一对应。 我们再回到原先的问题。 这里先给出一个结论： 结论1： 对于n的阶乘n！，其因式分解中，如果存在一个因子“5”，那么它必然对应着n！末尾的一个“0”。 下面对这个结论进行证明： (1)当n < 5时, 结论显然成立。 (2)当n >= 5时，令n！= [5k * 5(k-1) * ... * 10 * 5] * a，其中 n = 5k + r (0 <= r <= 4)，a是一个不含因子“5”的整数。 对于序列5k, 5(k-1), ..., 10, 5中每一个数5i(1 <= i <= k)，都含有因子“5”，并且在区间(5(i-1),5i)(1 <= i <= k)内存在偶数，也就是说，a中存在一个因子“2”与5i相对应。 即，这里的k个因子“5”与n！末尾的k个“0”一一对应。 我们进一步把n！表示为：n！= 5^k * k! * a（公式1），其中5^k表示5的k次方。 很容易利用(1)和迭代法，得出结论1。 上面证明了n的阶乘n！末尾的“0”与n！的因式分解中的因子“5”是一一对应的。 也就是说，计算n的阶乘n！末尾的“0”的个数，可以转换为计算其因式分解中“5”的个数。 令f(x)表示正整数x末尾所含有的“0”的个数, g(x)表示正整数x的因式分解中因子“5”的个数，则利用上面的的结论1和公式1有： f(n!) = g(n!) = g(5^k * k! * a) = k + g(k!) = k + f(k!) 所以，最终的计算公式为： 当0 < n < 5时，f(n!) = 0; 当n >= 5时，f(n!) = k + f(k!), 其中 k = n / 5（取整）。 计算举例 f(5!) = 1 + f(1!) = 1 f(10!) = 2 + f(2!) = 2 f(20!) = 4 + f(4!) = 4 f(100!) = 20 + f(20!) = 20 + 4 + f(4!) = 24 f(1000!) = 200 + f(200!) = 200 + 40 + f(40!) = 240 + 8 + f(8!) = 248 + 1 + f(1) =249

11111111111的阶乘是多少?

无法计算。 详细解释如下：首先，我们需要理解什么是阶乘。 阶乘是一个数学概念，通常表示为n!，它表示从1乘到n的所有正整数的乘积。 例如，5! = 5 × 4 × 3 × 2 × 1 = 120。 然而，当我们尝试计算一个非常大的数字的阶乘时，比如，我们很快会遇到问题。 首先，这个数字有11位，远远超出了我们日常计算的能力范围。 其次，即使使用计算机，这样的计算也会非常耗时，并且很容易超出计算机能够处理的范围。 更重要的是，当我们计算一个非常大的数字的阶乘时，结果会是一个非常大的数，远远超出了我们日常使用的数值范围。 这样的数通常被称为“天文数字”，因为它们的大小已经超出了我们的日常经验和想象。 因此，尽管我们可以尝试使用计算机来计算的阶乘，但实际上，这样的计算是不现实的，因为结果会是一个我们无法处理或理解的巨大数字。 所以，我们只能说，的阶乘是一个无法计算或表示的数。

1000的阶乘的结果里有多少个连续的0，怎么算？

每出现一个2和5，就会在末尾有一个0，所以只要看，从1到1000中总共有多少个2和5就可以了，又因为5总比2少，所以，只要看1000的阶乘中有多少个约数5就可以了。 同样，只有末尾是0或者5的数才会有5，所以总共只有200个数其中包含5，但是，其中有1000/25=40个数包含2个5，1000/125=8个数包含三个5，1000/625=1个数包含4个5,所以总共有200+40+8+1=249个5,所以结果里总共有249个连续的0。

求写一个简单算法，。 算1000的阶乘有多少个零

如果你说的是结果后面跟了多少个零，思路是用一个循环从1走到1000。 里面再套一个循环，整出10一次累积1，结果再除10如果能整出再累积1，随时不能整除就结束。 进行外部循环下一项。

---

---

相关标签： 1000的阶乘多少位、 从基本概念到惊人结果、 阐述千位阶乘、

上一篇：揭秘1000的阶乘数学和计算机科学的瑰宝揭秘

下一篇：计算和理解1000的阶乘数学与计算的交汇点计