(换肤)
语言：
概率密度函数：揭示随机变量的不确定性 (概率密度函数是什么)
03e假设X是一个服从正态分布的随机变量，其均值为50，标准差为10，那么，X落在40到60之间的概率为，P，40≤X≤60，=∫4060，1，√，2π102，e，x，50，2，2102，dx≈0.6827结论概率密度函数是描述连续随机变量不确定性的重要工具，它们在概率和统计中有着广泛的应用，可以帮助我们了解数据分布、计算概...。
互联网资讯 2024-09-13 07:15:28
γ 分布密度函数的数学基础：从基本原理到高级定理 (分布密度函数简写)
基本原理γ分布是一种连续概率分布，用于描述具有正实随机变量的各种现象，其概率密度函数，PDF，为，$$f，x，\alpha，\beta，=\frac，\beta^\alpha，\Gamma，\alpha，x^，\alpha，1，e^，\betax，$$其中，$x$是随机变量$\alpha$是形状参数$\beta$是速率参数$\G...。
本站公告 2024-09-09 08:38:06
探索 γ 分布密度函数的应用领域：从金融到工程 (分布密集)
引言Γ分布是一种连续概率分布，它以其广泛的形状和规模参数而闻名，使其具有高度的灵活性，由于其多功能性，Γ分布在金融、工程和统计等众多领域中有着广泛的应用，Γ分布密度函数Γ分布的概率密度函数为，f，x，=，λ^α，Γ，α，x^，α，1，e^，λx，其中，α是形状参数λ是尺度参数Γ，α，是Γ函数，定义为，Γ，α，=∫0^∞t^，α，1...。
最新资讯 2024-09-09 08:36:31
γ 分布密度函数的解读：从零到无限的探索之旅 (β分布密度函数)
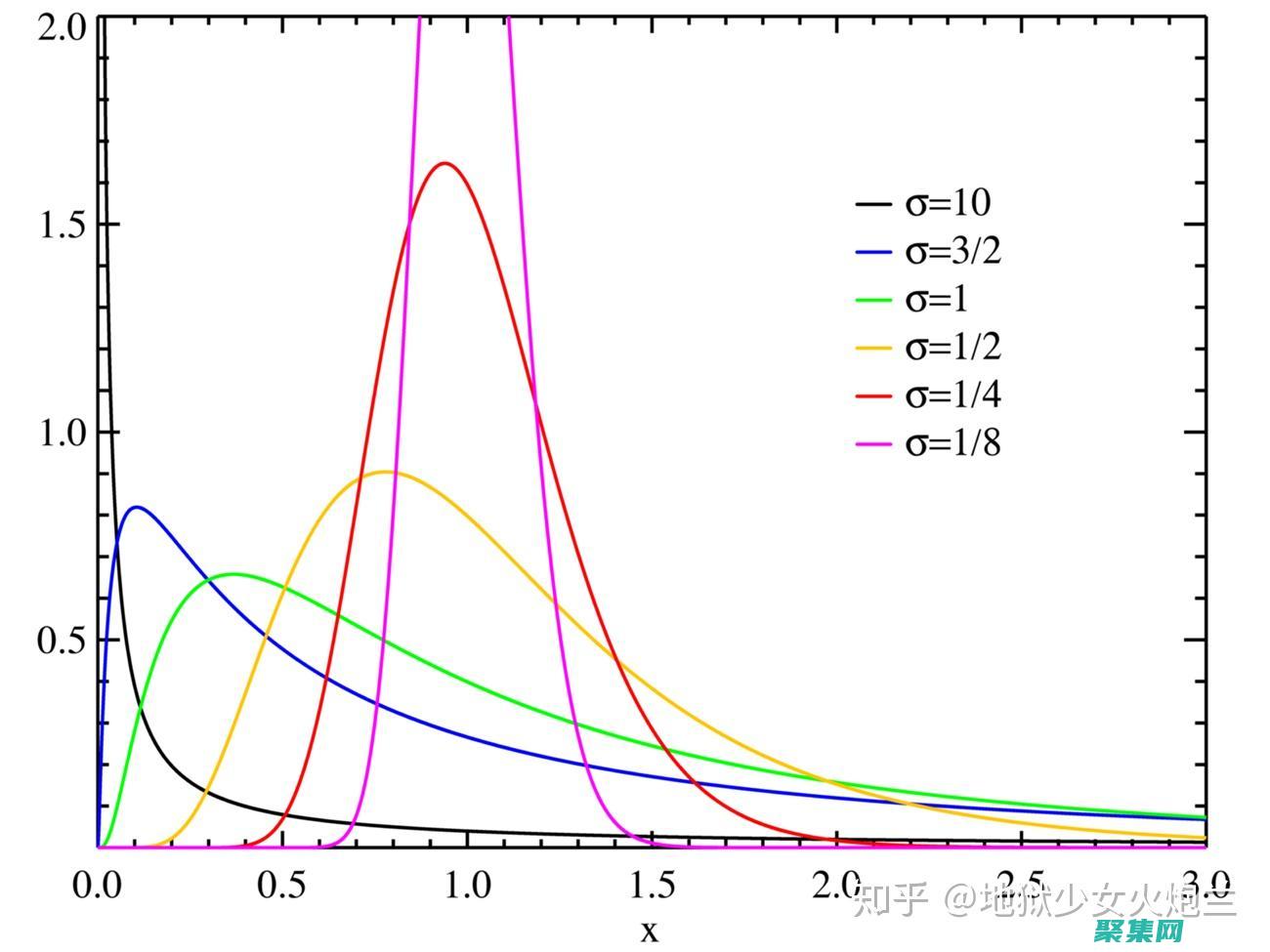
简介γ分布，又称伽马分布，是一种连续概率分布，广泛应用于概率论和统计学中，其概率密度函数被定义为，f，x，=，x^α，1，e^，x，β，Γ，α，β^α，其中，α和β分别为形状参数和尺度参数，Γ，·，为伽马函数，函数图像γ分布密度的形状取決于其形状参数α，α<，1，曲线向右偏，具有右尾比左尾更长的分布，α=1，曲线呈指数分布，...。
互联网资讯 2024-09-09 08:31:37
Gamma 函数的分布和统计应用：从随机变量到概率分布 (gamma函数)
简介Gamma函数是一个广义的阶乘函数，它将正实数映射到正实数，它在概率论和统计学中有着广泛的应用，特别是在连续概率分布和随机变量的建模中，Gamma分布Gamma分布是一个连续概率分布，其概率密度函数为，αxα，1e，αx，Γ，α，其中α是形状参数，x是随机变量，Gamma分布具有高度的可塑性，它可以模拟各种不同的形状，从指数衰减到...。
最新资讯 2024-09-08 12:23:38